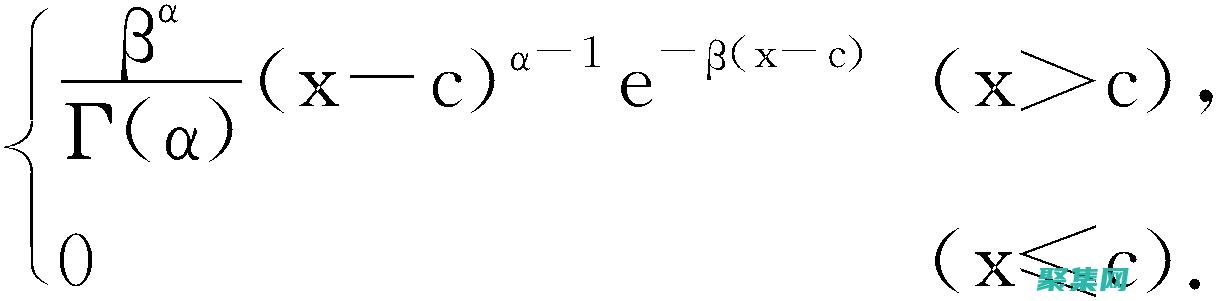 Γ(z)Γ(1-z) = π/sin(πz)(Γ(z)Γ(1-z))
Γ(z)Γ(1-z) = π/sin(πz)(Γ(z)Γ(1-z))
Γ函數,又稱伽馬函數,是一個推廣階乘函數到復平面的函數,它的定義如下,Γ,z,=∫0tz,1e,tdt對于正整數n,Γ,n,=,n,1,Γ函數滿足以下乘積公式,Γ,z,Γ,1,z,=π,sin,πz,這個公式可以用來求解許多積分,例如,∫0tα,1,1,t,β,1dt=B,α,β,Γ,α,Γ,β,其中B,α,β,是貝塔函數,證明我...。
技術教程 2024-09-12 13:42:55
 Γ(n) = (n-1)!(Γn+1)
Γ(n) = (n-1)!(Γn+1)
Γ,伽馬,函數是一種推廣階乘的概念,表示實數和復數的函數,它與階乘函數有密切的關系,可以通過將階乘函數連續化來獲得Γ函數,有關Γ函數的展開內容,請參閱維基百科的條目,Γ函數的遞推公式Γ函數具有以下遞推公式,Γ,n,=,n,1,其中,n是一個正整數,n,1,是,n,1,的階乘這個遞推公式表明,一個正整數的Γ函數值等于其前一個整數的階...。
互聯網資訊 2024-09-12 13:35:09
 gamma 函數表:探索其在積分、概率和特殊函數中的用法(gamma函數公式)
gamma 函數表:探索其在積分、概率和特殊函數中的用法(gamma函數公式)
Γ函數,伽馬函數,是一個廣義的階乘函數,具有以下性質,$$\Gamma,z,1,=z\Gamma,z,\quadz\in\mathbb,C,$$Γ函數在許多領域都有廣泛的應用,包括積分、概率和特殊函數,下表總結了Γ函數的一些重要公式和用法,公式用法$$\Gamma,z,=\int,0^\inftyt^,z,1,e^,t,dt,\q...。
互聯網資訊 2024-09-12 13:06:07
 階乘函數的延伸:探索伽馬函數和超越函數 (階乘函數解析延拓)
階乘函數的延伸:探索伽馬函數和超越函數 (階乘函數解析延拓)
引言階乘函數是一個定義在非負整數上的函數,表示一個數字的乘積與其所有較小正整數的乘積,例如,5的階乘,表示為5,為120,因為5,=5×4×3×2×1,階乘函數是一個基礎數學工具,在許多領域都有應用,包括組合學、概率和統計,階乘函數僅定義在非負整數上,限制了其應用范圍,為了克服這一限制,數學家開發了伽馬函數和超越函數等拓展函數,伽馬...。
互聯網資訊 2024-09-11 10:58:10
 階乘函數的高級概念:從漸近分析到矩陣乘法 (階乘函數高中學嗎)
階乘函數的高級概念:從漸近分析到矩陣乘法 (階乘函數高中學嗎)
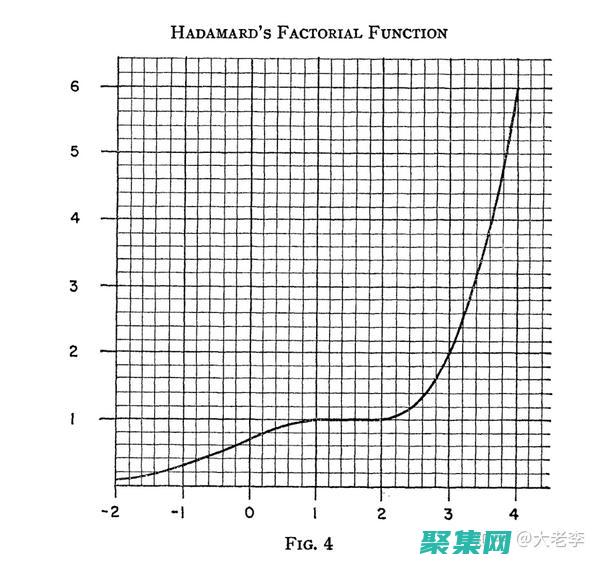
引言階乘函數,記作n,,是數學中一個基本函數,定義為從1到n的所有正整數的乘積,對于整數n≥1,n,計算為,```n,=1×2×3×...×n```階乘函數在數學和計算機科學中有著廣泛的應用,如組合、排列和概率論,本文將深入探討階乘函數的高級概念,包括漸近分析和矩陣乘法,漸近分析漸近分析涉及研究函數在大輸入值情況下的行為,對于階乘函數...。
本站公告 2024-09-11 10:56:55
 階乘函數在計算機科學中的角色:加密和信息處理 (階乘函數計算)
階乘函數在計算機科學中的角色:加密和信息處理 (階乘函數計算)
階乘函數簡介階乘函數,記作n,,表示正整數n的連續乘積,從1到n,例如,5,計算為5x4x3x2x1=120,階乘函數在數學和計算機科學中有廣泛的應用,在計算機科學中,它在加密和信息處理中特別有用,加密階乘函數是RSA加密算法的基礎,該算法是當今最廣泛使用的公共密鑰加密系統之一,RSA算法使用兩個大素數作為公鑰,而私鑰是由這兩個素數的...。
本站公告 2024-09-11 10:55:40
 階乘函數與自然界的聯系:從物理學到生物學 (階乘函數是初等函數嗎)
階乘函數與自然界的聯系:從物理學到生物學 (階乘函數是初等函數嗎)
階乘函數,表示為n,,定義為從1到n的所有正整數的乘積,它在數學和科學的各個領域都有廣泛的應用,從基礎物理學到復雜的生物過程,物理學統計力學,階乘函數用于計算微觀狀態的數量,這些狀態具有相同的宏觀特性,例如,它用于計算給定體積和溫度條件下的氣體分子的微觀分布,量子力學,階乘函數用于計算波函數在勢壘上的反射和透射系數,這對于理解量子隧穿...。
互聯網資訊 2024-09-11 10:54:34
 階乘函數的特殊值:揭開神秘的數列 (階乘函數的算法)
階乘函數的特殊值:揭開神秘的數列 (階乘函數的算法)
引言階乘函數是一項基本的數學函數,廣泛應用于組合學、概率和數論等多個領域,階乘函數的定義如下,n,=1×2×3×...×n其中,n是一個自然數,階乘函數具有以下幾個重要的特殊值,0,=11,=12,=23,=64,=245,=1206,=7207,=50408,=403209,=36288010,=3628800階乘函數的算法計算階乘...。
互聯網資訊 2024-09-11 10:53:16
 階乘函數的計算技巧:優化效率和簡化復雜性 (階乘函數計算器)
階乘函數的計算技巧:優化效率和簡化復雜性 (階乘函數計算器)
引言階乘函數是一個基本數學函數,用于計算給定正整數的乘積,雖然階乘函數的計算看似簡單,但對于大整數而言,直接計算可能效率低下且容易出錯,本篇文章將介紹各種階乘函數計算技巧,以優化效率和簡化計算過程,遞推公式對于正整數n,階乘n,可以使用以下遞推公式計算,```n,=n,n,1,```例如,5,可以通過以下計算,```5,=54,4,...。
最新資訊 2024-09-11 10:52:06
 階乘函數在數學中的應用:從排列和組合到分析 (階乘函數怎么求導)
階乘函數在數學中的應用:從排列和組合到分析 (階乘函數怎么求導)
引言階乘函數是一個基本而重要的數學函數,它定義為正整數n的階乘是所有小于或等于n的正整數的乘積,階乘函數通常表示為n,例如,5,被計算為5×4×3×2×1=120,階乘函數在數學的許多領域都有應用,包括排列和組合、分析學、概率論和統計學,本文將探討階乘函數的一些主要應用,并重點介紹求階乘函數導數的方法,排列和組合階乘函數在排列和組合...。
互聯網資訊 2024-09-11 10:51:09
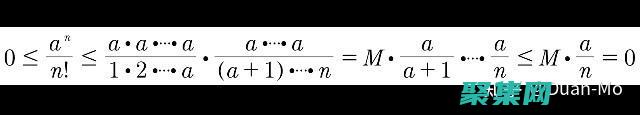 階乘函數簡介:了解其性質、公式和計算方法 (階乘函數的算法)
階乘函數簡介:了解其性質、公式和計算方法 (階乘函數的算法)
階乘函數是一種數學函數,它將正整數映射到正整數,表示從1到該整數的所有正整數的乘積,階乘符號為感嘆號,階乘函數的性質0,=1n,=n,n,1,n,1,=n,n,1,階乘函數的公式階乘函數的遞歸公式為,n,=n,n,1,其中,n是正整數,階乘函數的封閉公式為,n,=123...n階乘函數的計算方法遞歸算法deffacto...。
互聯網資訊 2024-09-11 10:49:40
 解開階乘函數的奧秘:從定義到實際應用 (如何解階乘方程)
解開階乘函數的奧秘:從定義到實際應用 (如何解階乘方程)
簡介階乘函數是一個數學函數,用于計算自然數的連續乘積,它表示為n,,其中n是一個非負整數,階乘函數在數學、科學和計算機科學等多個領域都有廣泛應用,定義階乘函數可以遞歸地定義為,```n,=1,如果n=0n,=n,n,1,,如果n>,0```例如,5,可以通過如下方式計算,```5,=54,=543,=5432,=54321,=5...。
最新資訊 2024-09-11 10:48:16
 階乘函數:深入探討數學中的基本運算 (階乘函數的算法)
階乘函數:深入探討數學中的基本運算 (階乘函數的算法)
階乘函數是數學中一個基本運算,用于計算一個自然數的階乘,階乘,通常表示為n,,是將給定數n與小于或等于n的所有正整數相乘得到的結果,例如,5的階乘,5,等于5×4×3×2×1=120,階乘函數的定義階乘函數可以用以下方式遞歸定義,0,=1n,=n×,n,1,這意味著0的階乘為1,任何其他自然數的階乘都等于該數乘以其前一個數的階乘,...。
最新資訊 2024-09-11 10:47:10
 Gamma 函數的分布和統計應用:從隨機變量到概率分布 (gamma函數)
Gamma 函數的分布和統計應用:從隨機變量到概率分布 (gamma函數)
簡介Gamma函數是一個廣義的階乘函數,它將正實數映射到正實數,它在概率論和統計學中有著廣泛的應用,特別是在連續概率分布和隨機變量的建模中,Gamma分布Gamma分布是一個連續概率分布,其概率密度函數為,αxα,1e,αx,Γ,α,其中α是形狀參數,x是隨機變量,Gamma分布具有高度的可塑性,它可以模擬各種不同的形狀,從指數衰減到...。
最新資訊 2024-09-08 12:23:38
 Gamma 函數與特殊函數之間的聯系:一個深入的探索 (gamma函數)
Gamma 函數與特殊函數之間的聯系:一個深入的探索 (gamma函數)
Gamma函數在數學領域中有著廣泛的應用,它與許多特殊函數有著密切的聯系,本文將深入探討Gamma函數與這些特殊函數之間的關系,揭示其內在的關聯性,伽馬函數的定義伽馬函數是一個解析函數,用于擴展階乘函數到復數域,它定義為以下積分,Γ,z,=∫0tz,1e,tdt其中z是復數,Gamma函數與階乘函數Gamma函數與階乘函數密切相關,當...。
技術教程 2024-09-08 12:21:06
 深入研究 Gamma 函數的積分性質 (深入研究崗位職責)
深入研究 Gamma 函數的積分性質 (深入研究崗位職責)
Gamma函數是一個重要的特殊函數,在數學和物理學中有廣泛的應用,本文將深入探討Gamma函數的積分性質,包括以下內容,Gamma函數的定義和基本性質Gamma函數的積分表示Gauss超幾何函數的積分表示MeijerG函數的積分表示應用示例Gamma函數的定義和基本性質Gamma函數是階乘函數f,x,=x,的解析延拓,對于復數z,定義...。
最新資訊 2024-09-08 12:19:08
 揭開 Gamma 函數的神秘面紗:從定義到性質 (揭開膏藥可以直接洗澡嗎)
揭開 Gamma 函數的神秘面紗:從定義到性質 (揭開膏藥可以直接洗澡嗎)
Gamma函數,記作Γ,z,,是數學中一個重要的特殊函數,具有深遠的理論和應用意義,它可以被看作階乘函數在復數域上的推廣,在概率、統計、物理和工程等領域有著廣泛的應用,1.定義Gamma函數的定義如下,其中,z是一個復數,且Re,z,>,0,2.性質Gamma函數具有許多重要的性質,包括,自變量關系,Γ,z,1,=zΓ,z,因子分...。
本站公告 2024-09-08 12:15:39