Γ函數(shù)，又稱伽馬函數(shù)，是一個推廣階乘函數(shù)到復平面的函數(shù)。它的定義如下：

Γ(z) = ∫ ₀ t ^z-1 e ^-t dt

對于正整數(shù)n，Γ(n) = (n-1)!

Γ函數(shù)滿足以下乘積公式：

Γ(z)Γ(1-z) = π/sin(πz)

這個公式可以用來求解許多積分，例如：

∫ ₀ t ^α-1 (1+t) ^β-1 dt = B(α, β)/Γ(α)Γ(β)

其中B(α, β)是貝塔函數(shù)。

證明

我們可以使用Γ函數(shù)的積分定義來證明乘積公式：

Γ(z)Γ(1-z) = ∫ ₀ e ^-t t ^z-1 dt ∫ ₀ e ^-u u ^-z du

令t = u，我們得到：

Γ(z)Γ(1-z) = ∫ ₀ e ^-t t ^z-1 t ^-z dt

這進一步簡化為：

Γ(z)Γ(1-z) = ∫ 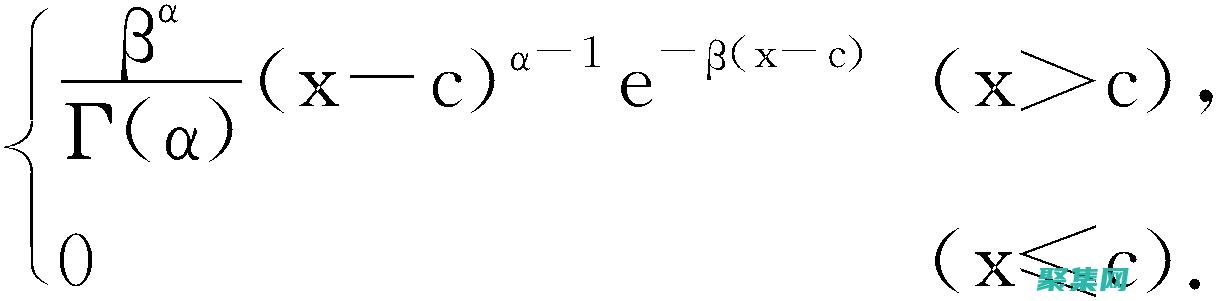₀ e ^-t dt

結(jié)果等于1，因此我們有：

Γ(z)Γ(1-z) = 1

再除以sin(πz)，我們得到：

Γ(z)Γ(1-z) = π/sin(πz)

這就是我們要證明的公式。

應(yīng)用

Γ函數(shù)的乘積公式在數(shù)學和物理中有著廣泛的應(yīng)用，包括：

• 求解積分
• 研究復分析
• 概率論和統(tǒng)計學
• 量子力學

這是一個非常有用的公式，它可以幫助我們解決許多復雜的問題。

---

---

相關(guān)標簽： Γ、 πz、 1、 Γ、 sin、 z、 z、 π、 1、 z、 z、 Γ、 =、 Γ、

上一篇：程序設(shè)計模式探索軟件設(shè)計的最佳實踐程序設(shè)

下一篇：Γnn1Γn1