文章編號:10975時間:2024-09-29人氣:
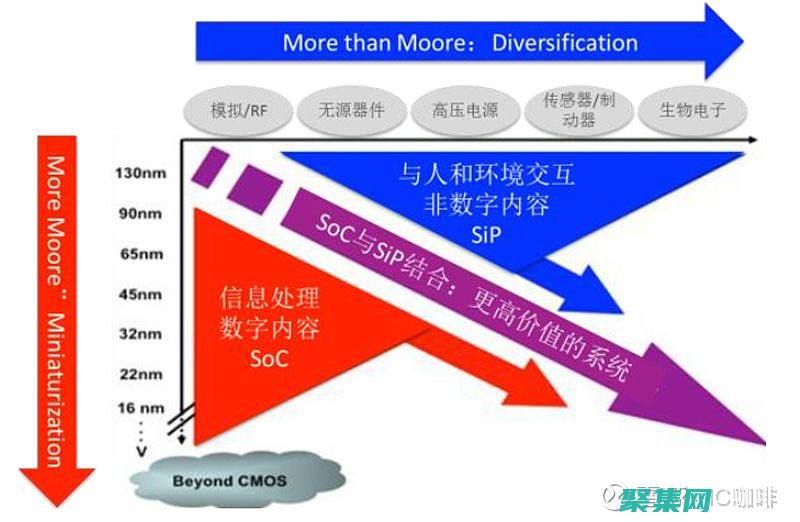
多項式回歸是一種機器學習算法,用于擬合基于多項式函數的數據。它是一種強大的工具,可用于對各種現象進行建模,例如增長模式、趨勢和周期。
流行的多項式回歸方法(如 polyfit)存在一些局限性。這些方法通常容易過擬合,并且可能對噪聲數據敏感。它們只能擬合低階多項式,這限制了它們的適用性。
為了克服這些限制,本文將探討多項式回歸的替代方法和擴展。這些方法提供了更好的擬合度、魯棒性和靈活性,可用于擬合更高階多項式。
正交多項式回歸使用正交多項式作為基函數。這些多項式是相互正交的,這意味著它們的點積為 0。這消除了多重共線性問題,提高了模型的魯棒性和穩定性。
拉普拉斯回歸使用拉普拉斯算子作為正則化項。該算子懲罰函數曲率的二階導數,從而產生平滑的多項式擬合。這有助于減少過擬合并提高模型的泛化能力。
貝葉斯多項式回歸將貝葉斯統計應用于多項式回歸。它通過對多項式系數的后驗分布進行推理,為模型參數提供了概率解釋。這允許對預測的不確定性進行量化,并促進模型選擇。
加權多項式回歸通過為不同的數據點分配權重來擴展多項式回歸。這允許強調重要的數據點并降低異常值的影響。權重可以根據數據點的置信度、噪聲水平或其他相關因素來確定。

廣義多項式回歸將多項式回歸擴展到非正態響應變量。它允許使用非線性聯接函數將多項式模型與各種概率分布相關聯。這增加了多項式回歸模型的適用性,使其可以用于分類、回歸和計數數據。
分段多項式回歸將數據分成多個子區間,并在每個子區間內擬合單獨的多項式。這允許在數據具有不同的線性或非線性趨勢的不同區域內捕獲復雜模式。分段多項式回歸可用于處理斷點、異常值和局部極值。
超越 polyfit 提供了多種替代方法和擴展,以增強多項式回歸的擬合度、魯棒性和靈活性。這些方法消除了過擬合,提高了預測精度,并擴大了多項式回歸對各種數據類型的適用性。
在選擇多項式回歸方法時,考慮數據的性質、擬合目標和模型的復雜性至關重要。替代方法和擴展提供了強大的工具,可用于探索復雜模式并從數據中提取有意義的見解。

1.基本概念多項式回歸(Polynomial Regression)是研究一個因變量與一個或多個自變量間多項式的回歸分析方法。 如果自變量只有一個 時,稱為一元多項式回歸;如果自變量有多個時,稱為多元多項式回歸。 ?1.在一元回歸分析中,如果依變量y與自變量x的關系為非線性的,但是又找不到適當的函數曲線來擬合,則可以采用一元多項式回歸。 2.多項式回歸的最大優點就是可以通過增加x的高次項對實測點進行逼近,直至滿意為止。 3.事實上,多項式回歸可以處理相當一類非線性問題,它在回歸分析 中占有重要的地位,因為任一函數都可以分段用多項式來逼近。 ?2.實例我們在前面已經根據已知的房屋成交價和房屋的尺寸進行了線 性回歸,繼而可以對已知房屋尺寸,而未知房屋成交價格的實例進行了成 交價格的預測,但是在實際的應用中這樣的擬合往往不夠好,因此我們在 此對該數據集進行多項式回歸。 目標:對房屋成交信息建立多項式回歸方程,并依據回歸方程對房屋價格進行預測 ?import as pltimport numpy as npfrom sklearn importlinear_model#導入線性模型和多項式特征構造模塊from importPolynomialFeaturesDatasets_X =[]datasets_Y =[]fr =open(,r)#一次讀取整個文件。 lines =()#逐行進行操作,循環遍歷所有數據for line in lines:#去除數據文件中的逗號items =()(,)#將讀取的數據轉換為int型,并分別寫入datasets_X和datasets_Y。 )(X,lin_reg_(poly__transform(X)),color=blue)(Area)(Price)()運行結果:Cofficients: [0.e+00 4.e-02 1.e-05]intercept 151.44通過多項式回歸擬合的曲線與 數據點的關系如下圖所示。 依據該 多項式回歸方程即可通過房屋的尺 寸,來預測房屋的成交價格。 ?文章知識點與官方知識檔案匹配Python入門技能樹人工智能基于Python的監督學習 人正在系統學習中打開CSDN,閱讀體驗更佳基于Python的多項式擬合方法_飄羽的博客_python 多項式...基于Python的多項式擬合方法 1. 直接上代碼進行介紹 __author__ =Administrator # coding=utf8 # 導入相關包 importnumpyasnp frompandasimportread_csv 2_score...繼續訪問python機器學習 | 多項式回歸和擬合_Claire_chen_jia的博客...多項式回歸中,加入了特征的更高次方(例如平方項或立方項),也相當于增加了模型的自由度,用來捕獲數據中非線性的變化。 多項式擬合lm_sklearn之多項式回歸 weixin_的博客 601 多項式回歸:若希望回歸模型更好的擬合訓練樣本...繼續訪問最新發布 Python回歸預測建模實戰-多項式回歸預測房價(附源碼和實現效果)Python回歸預測建模實戰-多項式回歸預測房價(附源碼和實現效果)繼續訪問?sklearn實現非線性回歸模型sklearn實現非線性回歸模型 前言: sklearn實現非線性回歸模型的本質是通過線性模型實現非線性模型,如何實現呢?sklearn就是先將非線性模型轉換為線性模型,再利用線性模型的算法進行訓練模型。 一、線性模型解決非線性模型的思想 1、樣本數據如下 x y 1 2 3 4 5 6 ...繼續訪問?多項式擬合,模型的復雜度以及權重的變化_今晚打佬虎的博客,提供了多項式特征的方法: X=(6)(3,2)poly=PolynomialFeatures(2)_transform(X)>>>array([[1.,0.,1.,0.,0.,1.],[1.,2.,3.,4.,6.,9...繼續訪問python數據處理三:使用sklearn實現曲線擬合_耐心的小黑的博客-CSDN博 _model import LinearRegressionfrom import PolynomialFeaturesimport numpy as npimport as plt#獲取待擬合數據x = (1, 50, 50)f = 1d([2,5,10])y ...繼續訪問機器學習(十)線性&多項式回歸之房價與房屋尺寸關系一.線性回歸 (1)線性回歸 ? 線性回歸(Linear Regression)是利用數理統計中回歸分析,來確定兩種或兩種以上變量間相互依賴的定量關系的一種統計分 析方法。 ? 線性回歸利用稱為線性回歸方程的最小平方函數對一個或多個自變量和因變量之間關系進行建模。 這種函數是一個或多個稱為回歸系數的模型參數的線性組合。 只有一個自變量的情況稱為簡單回歸,大于一個自變量情況的叫做多元回歸 線性回歸:使用形如y=w T x+b的線性模型擬合數據輸入和輸出之間的映射關系的。 線性回歸有很多實際的用途,分為以下兩類: 1.如果目標是預測或者映射,線性回歸可以用來對觀測數據集的y和X的值擬合出一個預測模型。 python完成非線性擬合在之前的博客使用python來完成數據的線性擬合當中,介紹了基于python,使用三種方法完成線性擬合的理論和代碼實現。 同樣經常會碰到樣本分布呈現非線性關系的情況,那么如何擬合出來呢?本文側重對數據已經有建模,但是準確的關系需要得以確定的情況。 如果想直接求出擬合系數,而不清楚原本模型的話,直接利用theta = (X, Y_noise, deg=4)得到y=a*x^4+b*x^3+c*x^2+d方程的theta=[a,b,c,d]。 這里deg=4表...繼續訪問?sklearn實現多項式回歸_盛夏未來的博客sklearn實現多項式回歸 多項式回歸 一個數據集,用散點圖畫出來如下圖,可以看到此時用一條直線(或者超平面)是不能擬合的,所以需要用一個多項式表示的曲線(或者超曲面)才能得到更好的擬合結果。 繼續訪問多項式回歸+房價與房屋尺寸的非線性擬合多項式回歸 多項式回歸(Polynomial Regression)是研究一個因變量與一個或多個自變量間多項式的回歸分析方法。 如果自變量只有一個時,稱為一元多項式回歸;如果自變量有多個時,稱為多元多項式回歸。 在一元回歸分析中,如果依變量y與自變量X的關系為非線性的,但是又找不到適當的函數曲線來擬合,則可以采用一元多項式回歸。 后續的實例就是這個例子。 多項式回歸的最大優點就是可以通過增加X的高次...繼續訪問Python機器學習應用 | 多項式回歸1 多項式回歸多項式回歸(Polynomial Regression)是研究一個因變量與一個或多個自變量間多項式的回歸分析方法。 如果自變量只有一個時,稱為一元多項式回歸;如果自變量有多個時,稱為多元多項式回歸。 在一元回歸分析中,如果依變量y與自變量x的關系為非線性的,但是又找不到適當的函數曲線來擬合,則可以采用一元多項式回歸。 多項式回歸的最大優點就是可以通過增加x的高次項對實測點進行逼近,直繼續訪問多項式擬合lm_sklearn之多項式回歸多項式回歸:若希望回歸模型更好的擬合訓練樣本數據,可以使用多項式回歸器。 一元多項式回歸:數學模型:y = w0 + w1 * x^1 + w2 * x^2 + .... + wn * x^n將高次項看做對一次項特征的擴展得到:y = w0 + w1 * x1 + w2 * x2 + .... + wn * xn那么一元多項式回歸即可以看做為多元線性回歸,可以使用LinearRegressio...繼續訪問sklearn多項式擬合繼續訪問【Scikit-Learn】多項式擬合%matplotlib inline import as plt import numpy as np n_dots = 20 x = (0, 1, n_dots) # [0, 1] 之間創建 20 個點 y = (x) + 0.2*(n_dots) - 0....繼續訪問python 非線性多項式擬合_淺析多項式回歸與sklearn中的Pipeline0x00 前言 之前我們介紹了簡單線性回歸,其輸入特征只有一維,即:;推廣到多維特征,即多元線性回歸:。 但是在線性回歸的背后是有一個很強的假設條件:數據存在線性關系。 但是更多的數據之間具有非線性關系。 因此對線性回歸法進行改進,使用多項式回歸法,可以對非線性數據進行處理。 0x01 什么是多項式回歸 研究一個因變量與一個或多個自變量間多項式的回歸分析方法,稱為多項式回歸(Polynomial...繼續訪問?機器學習-sklearn-多項式回歸-對函數擬合-看學習曲線(均方誤差MSE)-pipelinepython sklearn pipeline做函數擬合,-看學習曲線(均方誤差MSE)繼續訪問?sklearn實現多項式回歸1)生成數據集 import numpy as np import as plt n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5 # X = (-3,3,n_train+n_test) X = (size=(n_train...繼續訪問多項式回歸線性回歸只能擬合簡單的 線性問題,當現在數據的復雜程度不能使用線性擬合,這時要考慮非線性擬合。 現在考慮一種最簡單的非線性擬合--多項式回歸。 多項式回歸的含義是直接從線性回歸過度到非線性,簡單的做法可以將原來的特征的冪次方作為一個新的特征,這樣隨著特征的逐漸復雜,它也能夠解決非線性數據的擬合問題,這種從線性特征集上擴展過來的模型,稱為多項式回歸。 首先創建非線性帶噪聲的數據集 import...繼續訪問?sklearn多項式回歸# -*- coding: utf-8 -*- Created on Mon Jan 29 22:57:10 2018 @author: Administrator import as plt import numpy as np from _model import LinearRegression#導入線性回歸繼續訪問【機器學習】多項式回歸python實現使用python實現多項式回歸,沒有使用sklearn等機器學習框架,目的是幫助理解算法的原理。 使用一個簡單的數據集來模擬,只有幾條數據。 代碼 從數據集中讀取X和y。 為X添加二次方項,用Z替換。 給Z添加 1 列,初始化為 1 ,用來求偏置項。 劃分訓練集和測試集。 將Z和y的訓練集轉換為矩陣形式。 和線性回歸類似,使用正規方程法,先驗證矩陣的可逆性。 去掉Z中全為1的列。 使用測試集...繼續訪問?sklearn線性回歸完成多次項函數和正弦函數擬合這樣兩個式子,使用sklearn 線性回歸進行擬合 直接上代碼 得到結果:score : 0. mse : 7940.3畫圖結果:對于正玄曲線原始數據畫圖 degree定成三階擬合圖 degree定成二階擬合圖degree定成六階擬合圖,效果非常好,但不知道是不是有點過擬合了、? 話不多說,直接上代碼:...繼續訪問?熱門推薦 python運用sklearn進行數據擬合和回歸在上一篇講了最小二乘法實現線性回歸的原理,實現方面用的是python的中的leastsq求出擬合函數。 本篇通過sklearn庫中的模塊來進行擬合和線性回歸,并計算擬合誤差。 對于線性回歸來說,無論是用什么工具實現,步驟都是大同小異的: 初始化多項式方程 對多項式方程進行多次迭代,通過最小二乘法求出使平方損失函數最小情況下的擬合方程。 對模型預測結果進行評估 調整參數...繼續訪問?sklearn-多項式回歸import numpy as np import as plt from import PolynomialFeatures from _model import LinearRegression #載入數據 data = (,delim...繼續訪問[機器學習與scikit-learn-31]:算法-回歸-線性模擬擬合擬合非線性數據-概述作者主頁(文火冰糖的硅基工坊):文火冰糖(王文兵)的博客_文火冰糖的硅基工坊_CSDN博客 本文網址: 目錄 第1章 什么是線性與非線性關系 1.1 描述對象 1.2 什么是線性與非線性關系 第2章 數據(分布)的線性與非線性 2.1 什么是線性與非線性數據(擬合、模擬回歸) 2.2什么是線性與非線性可分數據(分類、邏輯回歸) 2.3 分類問題的擬合表達 第3章 模型的線性與非線性 3.1 線性模型 3.2 特定的非線性模型 3.3 通用的非線性模型:多項式非線性模型(Polyn.繼續訪問
內容聲明:
1、本站收錄的內容來源于大數據收集,版權歸原網站所有!
2、本站收錄的內容若侵害到您的利益,請聯系我們進行刪除處理!
3、本站不接受違法信息,如您發現違法內容,請聯系我們進行舉報處理!
4、本文地址:http://www.lmxpnzry.com/article/0e321f7fbe0991affd25.html,復制請保留版權鏈接!

網購已經成為人們生活中不可或缺的一部分,而隨之而來的快遞物流問題也讓人頭疼不已,焦急地等待快遞,不知何時才能收到,這種感覺實在令人抓狂,為了解決這一痛點,本文將介紹一款快遞跟蹤利器,幫助你輕松查詢快遞信息,告別焦急等待,一、快遞跟蹤利器是什么快遞跟蹤利器是一款提供快遞物流查詢服務的工具,它集成各大快遞公司的查詢接口,讓你只需輸入快遞單...。
本站公告 2024-09-27 15:29:51
超鏈接顏色是網站設計中至關重要的元素,因為它負責引導用戶瀏覽網站,選擇正確的顏色方案可以增強網站的可用性和視覺吸引力,本文將探討超鏈接顏色策略,以幫助您建立有效的網站導航和視覺分層,超鏈接顏色的重要性超鏈接顏色對于網站的可用性和用戶體驗至關重要,通過使用清晰易辨的顏色,用戶可以輕松識別可點擊的元素并瀏覽網站,超鏈接顏色還可以用于創建視...。
技術教程 2024-09-25 14:30:24
前言在當今快速發展的數字環境中,網站的速度和效率至關重要,一個快速加載的網站不僅可以提升用戶體驗,還可以對搜索引擎優化,SEO,和網站的整體成功產生積極影響,而文件大小是影響網站速度的主要因素之一,文件大小與網站速度較大的文件需要更長的時間來加載,從而導致網站速度變慢,當用戶訪問速度較慢的網站時,他們更有可能被勸退并轉到其他網站,根據...。
本站公告 2024-09-16 15:49:11
Yii是一個用于構建現代化Web應用程序的高性能PHP框架,它以其強大、靈活和易于使用的特點而聞名,在本指南中,我們將探索Yii框架的主要功能,并展示如何利用它們來創建健壯且可擴展的Web應用程序,架構Yii采用分層架構,將應用程序的不同組件分解為模塊化的塊,這種方法使您可以輕松地維護和更新您的應用程序,因為它允許您獨立于其他組件開發...。
最新資訊 2024-09-16 09:48:40

ReactXP是一個跨平臺框架,可幫助您使用JavaScript和React構建適用于iOS、Android和Web的原生應用程序,使用ZoomXZoomX是ReactXP的一個可選組件,它可以通過CSS,like語法提供對nativeZoomSDK的訪問,它允許您在ReactXP應用程序中輕松集成視頻會議功能,安裝ZoomX```b...。
技術教程 2024-09-16 01:45:36

掌握JSTL中的XML處理標簽,實現高效的數據處理概述JavaServerPagesStandardTagLibrary,JSTL,提供了一組標準標簽,用于簡化Web開發任務,其中,XML處理標簽允許開發者在JSP頁面中輕松處理和轉換XML數據,掌握這些標簽可以極大地提高數據處理效率和代碼可讀性,XML處理標簽JSTL提供了以下XML...。
互聯網資訊 2024-09-15 14:23:03

引言JavaScript是當今最流行的編程語言之一,而ES6是其最新版本,帶來了許多令人興奮的新特性,在文章中,我們將從阮一峰的角度來探索ES6的魅力,了解它如何推動JavaScript生態圈蓬勃發展,箭頭函數箭頭函數是ES6中引入的一種新的函數語法,與傳統函數相比,它更簡潔、更易于寫,箭頭函數沒有自己的`this`關鍵字,并且可以自...。
最新資訊 2024-09-14 21:36:02

序言在快速發展的數字金融時代,發卡運營已成為各行業企業提升競爭力和客戶忠誠度不可或缺的戰略舉措,傳統發卡系統往往難以滿足企業不斷增長的定制化需求,限制了發卡運營的靈活性,因此,采用全面源碼的發卡平臺變得至關重要,它賦予企業充分的自主權,實現發卡運營的全面自動化和高度定制,發卡控的意義發卡控是指企業對發卡業務的全面掌控能力,包括發卡流程...。
本站公告 2024-09-14 18:47:01

簡介時間是現代生活中一個不可忽視的要素,我們總是被各種截止時間和任務所包圍,管理時間并保持高效對于成功至關重要,倒計時代碼可以幫助我們控制時間,讓我們更有效地規劃和管理我們的時間,什么是倒計時代碼,倒計時代碼是一種計算機程序,允許我們創建視覺上吸引人的倒計時,顯示剩余時間或距離特定事件的持續時間,它們通常以數字、文字或圖形的形式顯示,...。
最新資訊 2024-09-09 04:35:09

歡迎來到我們的Windows游戲編程教程!在這個教程中,我們將一步一步地指導你創建一個屬于你自己的Windows游戲,即使你沒有編程經驗,也不必擔心,我們將從最基礎的概念開始,并逐步深入更高級的技術,步驟1,設置開發環境在開始編程之前,我們需要設置好開發環境,為此,我們需要以下軟件,MicrosoftVisualStudio2022,...。
互聯網資訊 2024-09-07 10:45:18

前言社交媒體已成為企業增長的必備工具,它提供了與目標受眾建立聯系、建立品牌知名度和推動銷售的強大平臺,社交媒體營銷環境不斷變化,因此企業必須了解最新趨勢并采用有效的策略才能獲得成功,本指南將為您提供社交媒體營銷前沿的全面透視,并提供解鎖增長的終極秘訣,社交媒體營銷趨勢1.短視頻的崛起短視頻平臺,如TikTok和InstagramRee...。
互聯網資訊 2024-09-06 22:12:46

在做網站優化的時候,經常會遇到很多問題,而出現的問題不僅會影響到用戶體驗,同時還影響到搜索引擎的收錄,從而導致網站排名不好,那么,網站優化中經常遇到的問題有哪些呢,1、網站關鍵詞定位不準確現在很多網站為了在搜索引擎中獲得好的排名,在網站中堆積了大量的關鍵詞,這樣不僅不利于網站優化,同時網站還有可能被搜索引擎懲罰,所以,網站在選擇關鍵詞...。
技術教程 2024-09-02 00:17:01